I’ve recently been working on creating AIs for games like chess and othello, and I’ve been putting a lot of thought into the move generation functions and search algorithms of these AIs. Since these components are run so many times, it’s important to make sure that they are very efficient so they don’t slow down the computer too much and impact the AIs performance.
Fortunately, I was able to implement few huge optimizations that drastically reduced the running time of my AI, which included a change in how the board is represented.
It turns out that instead of representing the positions of pieces on the game board with something like a 2d array, there’s a much more efficient data structure we can use: a bitboard.
Actually, multiple bitboards.
What I realized is that it’s much more efficient to represent the board simply as a collection of large numbers, instead of multi-dimensional arrays or some other complex structure.
In practice, what I mean by this is that we can take a 64 bit integer, called a bitboard, and assign each bit to a corresponding tile on a board like a chess board. By doing this, we can essentially store the board configuration using an integer, which takes up way less space in your computer’s memory than something like an array. Bitboards also have a couple other incredible advantages that I’ll dive into in a bit.
For example, In the game Othello, we might have 2 bitboards – 1 to represent the position of black pieces on the board and another for the white pieces. Each “on” bit, or 1, in a bitboard represents an occupied tile where a player’s piece is. Each “off” bit, or 0, represents an empty tile. This is why we have a bitboard for both black and white, to distinguish between each player’s pieces.
Defining a bitboard in C# can be as simple as declaring an unsigned (non-negative) long integer.
ulong bitboard = 0;
In a game like Othello, we can also create a class for the game board with attributes to hold the bitboards for black and white.
class Board
{
ulong white_pieces = 0;
ulong black_pieces = 0;
public Board()
{
white_pieces = 0x1008000000;
black_pieces = 0x810000000;
}
}
Now, if we initialize a new Board, it will give us the starting position for an Othello game.
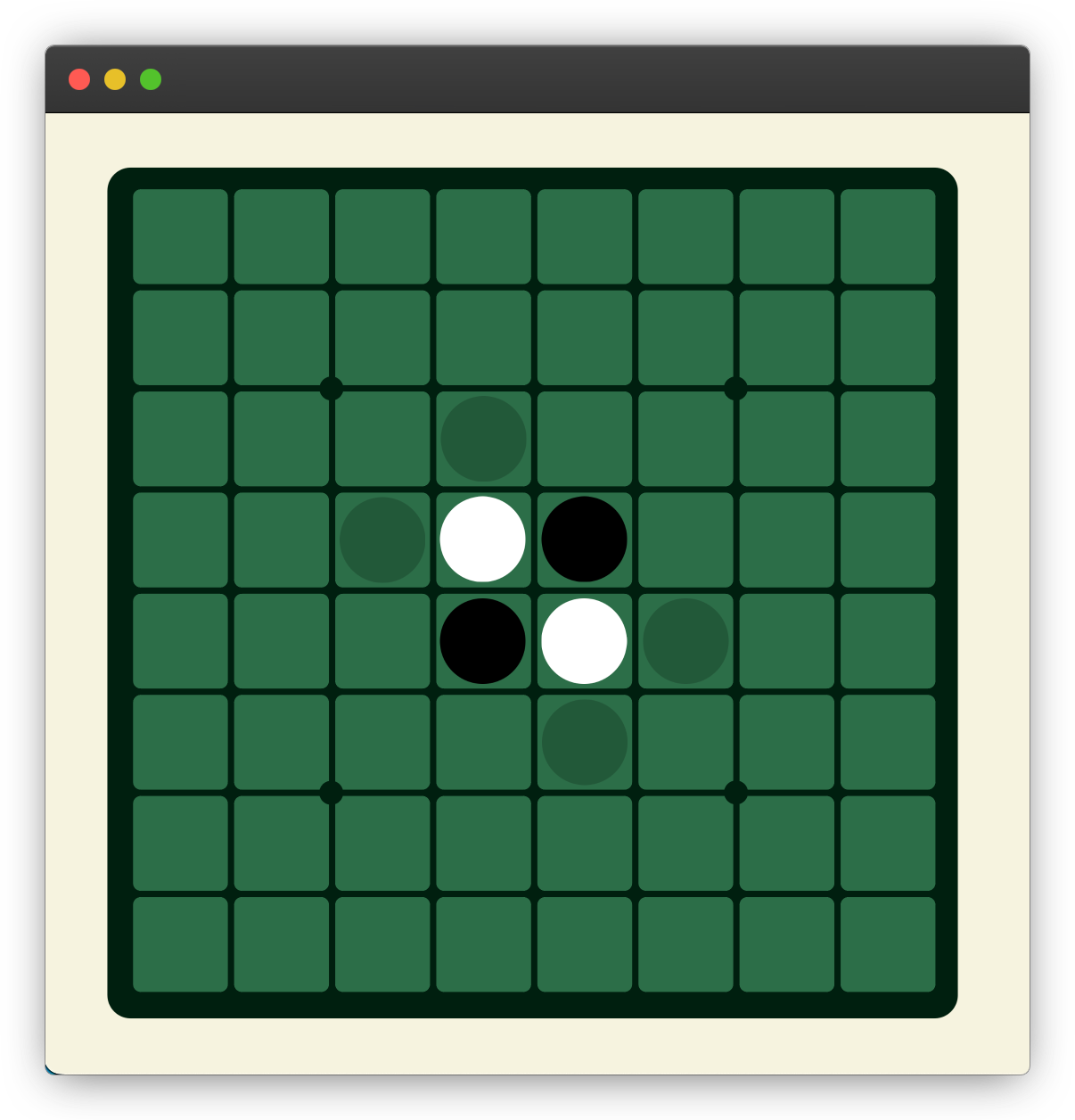
You can see that if you convert the values for white_pieces and black_pieces from hexadecimal to binary, the activated bits in each bitboard will line up with the positions of the pieces on the board.
ulong white_pieces = 0x1008000000;
/*
* 0x1008000000 = 0000000000000000000000000001000000001000000000000000000000000000
*
* 0 0 0 0 0 0 0 0
* 0 0 0 0 0 0 0 0
* 0 0 0 0 0 0 0 0
* 0 0 0 1 0 0 0 0
* 0 0 0 0 1 0 0 0
* 0 0 0 0 0 0 0 0
* 0 0 0 0 0 0 0 0
* 0 0 0 0 0 0 0 0
*/
ulong black_pieces = 0x810000000;
/*
* 0x810000000 = 0000000000000000000000000000100000010000000000000000000000000000
*
* 0 0 0 0 0 0 0 0
* 0 0 0 0 0 0 0 0
* 0 0 0 0 0 0 0 0
* 0 0 0 0 1 0 0 0
* 0 0 0 1 0 0 0 0
* 0 0 0 0 0 0 0 0
* 0 0 0 0 0 0 0 0
* 0 0 0 0 0 0 0 0
*/
Why use bitboards?
Well, I can assure you, though bitboards seem like a lot of hassle initially, they are well worth it for their performance benefits.
The primary reason why bitboards are so computationally efficient is because you can utilize bitwise operators to speed up calculation and eleminate conditionals.
Here’s an example:
In the game connect 4, in order to detect a win, we need to evaluate if either player has 4 in a row.
We can start by initializing two bitboards, one to keep track of the red player’s pieces and another to keep track of the yellow player’s pieces. Since a connect 4 board is smaller (only 42 tiles), we only need 42 bits to represent the board. So, we’ll assign each of the first 42 bits to a position on the board.
ulong red_pieces = 0;
ulong yellow_pieces = 0;
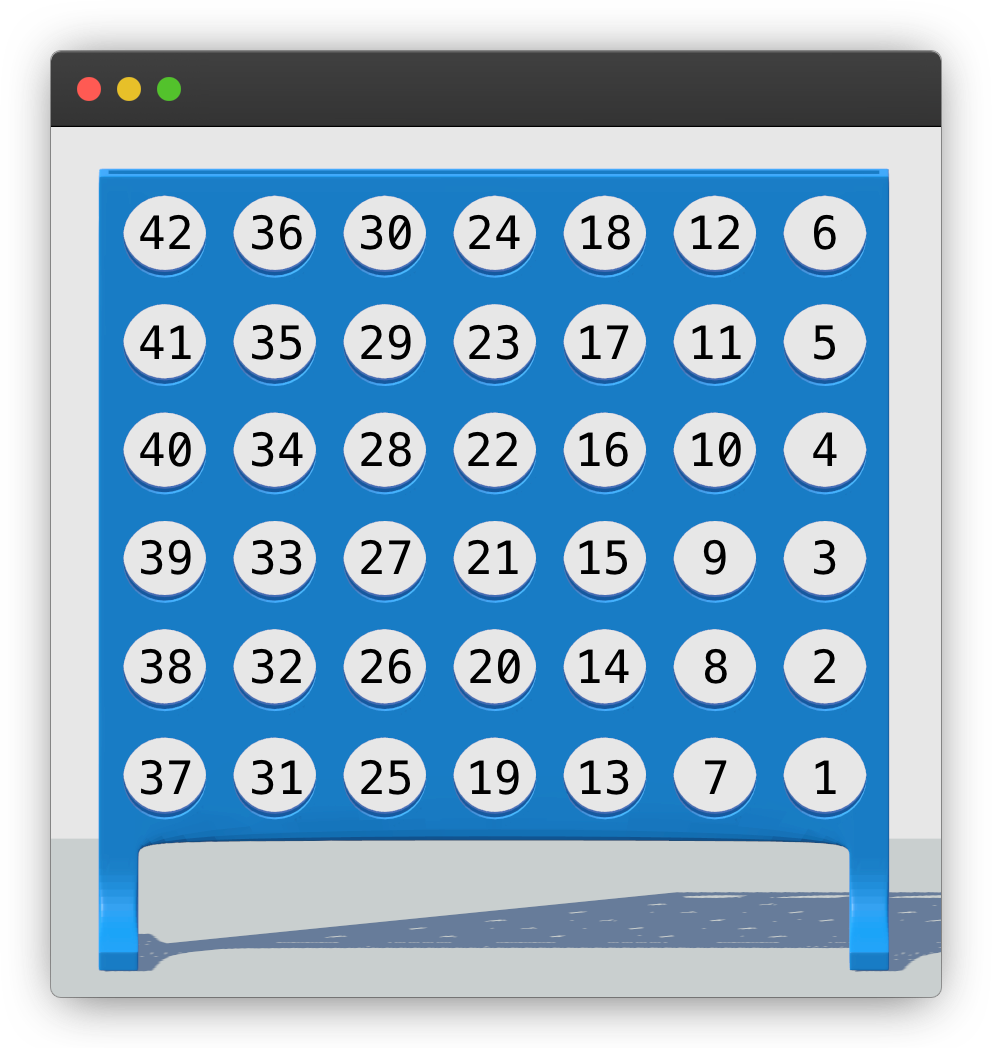
Now let’s assume the following board position:

As you can see in the above screenshot, yellow has won the game by placing 4 of their pieces vertically in a row.
Using a bitboard, we can check for a vertical win (in just 3 lines of code!) by utilizing the bitwise AND and bitshift operators as follows:
// Step 1:
ulong pairs = yellow_pieces & (yellow_pieces << 1);
// Step 2:
ulong quads = pairs & (pairs << 2);
// Step 3 – returning the result from steps 1 and 2:
return quads > 0
1. First of all, we start by initializing a new bitboard, called pairs.
The goal of this bitboard is to store all of the vertical pairs of yellow coins, all the 2-in-a-row combinations.
To do this, we first bitshift all the yellow pieces left 1 bit – the upwards direction.
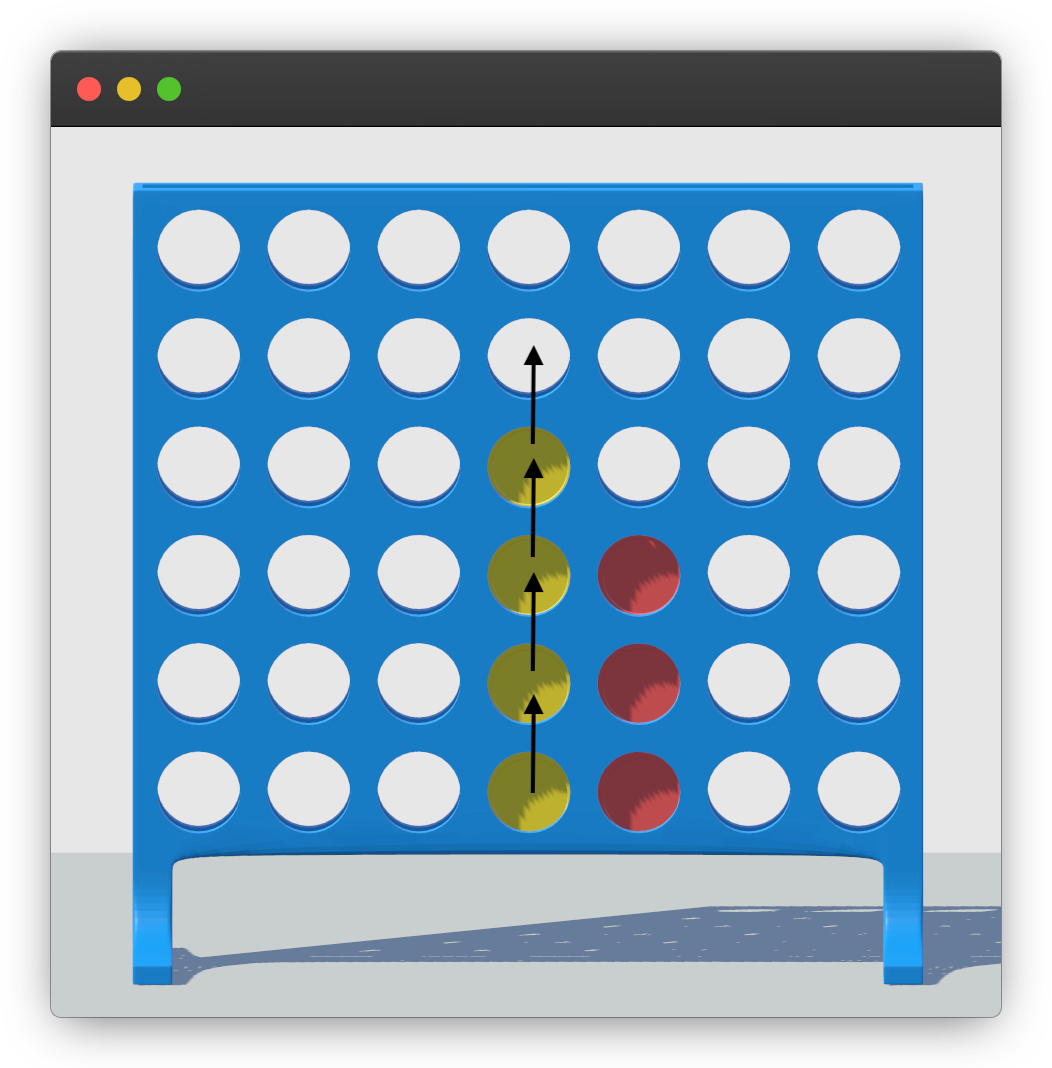
As you can see, bit 19 gets shifted to bit 20, bit 20 gets shifted to bit 21, bit 21 gets shifted to bit 22, and bit 22 gets shifted to bit 23.
Now that we have shifted all of the pieces up by 1 tile, we record which pieces align with the initial yellow pieces. If they do align, then we have found 2 in a row.
We can do this by using the bitwise AND operator.
/*
* 0 0 0 0 0 0 0 0 0 0 0 0 0 0
* 0 0 0 0 0 0 0 0 0 0 1 0 0 0
* 0 0 0 1 0 0 0 0 0 0 1 0 0 0
* 0 0 0 1 0 0 0 & 0 0 0 1 0 0 0
* 0 0 0 1 0 0 0 0 0 0 1 0 0 0
* 0 0 0 1 0 0 0 0 0 0 0 0 0 0
*/
// 000000000000000000001111000000000000000000 & 000000000000000000011110000000000000000000
Bits 20, 21, and 22 are activated on both bitboards, so when we AND them together, those are the bits that will be left on.
/*
* 0 0 0 0 0 0 0
* 0 0 0 0 0 0 0
* 0 0 0 1 0 0 0
* 0 0 0 1 0 0 0
* 0 0 0 1 0 0 0
* 0 0 0 0 0 0 0
*/
// 000000000000000000001110000000000000000000
Since there are three activated bits, we can see that there were three pairs of vertical yellow pieces.
2. Next, we’ll repeat the whole process again to find 4 in a row – with a slight tweak.
This time, we’re going to calculate a bitboard called quads – we’ll take the bitboard pairs that we just calculated and bitshift it left 2 bits. This is to find “pairs of pairs”, or 4 in a row.
// 000000000000000000001110000000000000000000 << 2
/*
* Result:
*
* 0 0 0 1 0 0 0
* 0 0 0 1 0 0 0
* 0 0 0 1 0 0 0
* 0 0 0 0 0 0 0
* 0 0 0 0 0 0 0
* 0 0 0 0 0 0 0
*/
// 000000000000000000111000000000000000000000
Finally, we’ll AND the result with pairs . If there are any bits left on after this operation, we’ll know we have found four in a row.
/*
* 0 0 0 1 0 0 0 0 0 0 0 0 0 0
* 0 0 0 1 0 0 0 0 0 0 0 0 0 0
* 0 0 0 1 0 0 0 0 0 0 1 0 0 0
* 0 0 0 0 0 0 0 & 0 0 0 1 0 0 0
* 0 0 0 0 0 0 0 0 0 0 1 0 0 0
* 0 0 0 0 0 0 0 0 0 0 0 0 0 0
*/
// 000000000000000000111000000000000000000000 & 000000000000000000001110000000000000000000
Result:
/*
* 0 0 0 0 0 0 0
* 0 0 0 0 0 0 0
* 0 0 0 1 0 0 0
* 0 0 0 0 0 0 0
* 0 0 0 0 0 0 0
* 0 0 0 0 0 0 0
*/
// 000000000000000000001000000000000000000000
1 bit (that corresponds to the topmost yellow piece) has been left activated - this means that we have found four in a row.
3. If no bits have been left activated, the value of quads will be 0, which is why we return true if quads is bigger than 1 - to signify a win.
To calculate four in a row in other directions too, we can just change the amount bitshifted. For example, we could calculate horizontal wins by bitshifting 6 bits to the left, instead of 1.
As you can see, using bitboards, we are able to calculate wins in connect 4 (and many other applications) without the use of many conditionals and using very low-level operations. This makes bitboards remarkably fast – good for an AI that needs to check for wins millions of times.
You can imagine how bitboards can also be applied to more complex games like chess, where you’d have a bitboard for each type of piece and color (i.e. A bitboard for white knights).
Check out my full Connect 4 AI and Othello AI.
