If you haven’t been following along with the previous posts in this neural networks series, I highly recommend reading those before continuing forward.

At this point in the series, we’ve talked about layers, and we’ve talked about coding neurons. Now, we’re going to scale up the neuron code to be applicable for layers of the network, to make it more customizable and functional.

Why are we doing this?

The reason we can’t just take the neuron code from Part 2 and move forward is because it isn’t really practical in the context of our network. If you recall, we created a class for each neuron in the network, but with neural networks getting increasingly large (most networks have thousands to millions of neurons), it’s simply too tedious and too slow to instantiate a new instance of the class for each neuron in the network. That approach might be manageable for the simple 6-neuron example network I presented, but it won’t be realistic for larger-scale networks with practical functionality.

Thus, we need to scale our neuron code to work with layers in our network.

What are we going to do instead?

Well, instead of having a class for each neuron in the network, it would be more realistic to define a class that represents each layer in the network.

Remember, networks can have any number of hidden layers, so by creating a class to represent network layers, we can make our network functional, practical, and scalable.

Alright, how is this going to work?

Well, in order to move forward, we’re going to need to change up how we’ve been thinking. We’ll need to start using matrices to describe things like weights and biases.

For example, consider the following model:

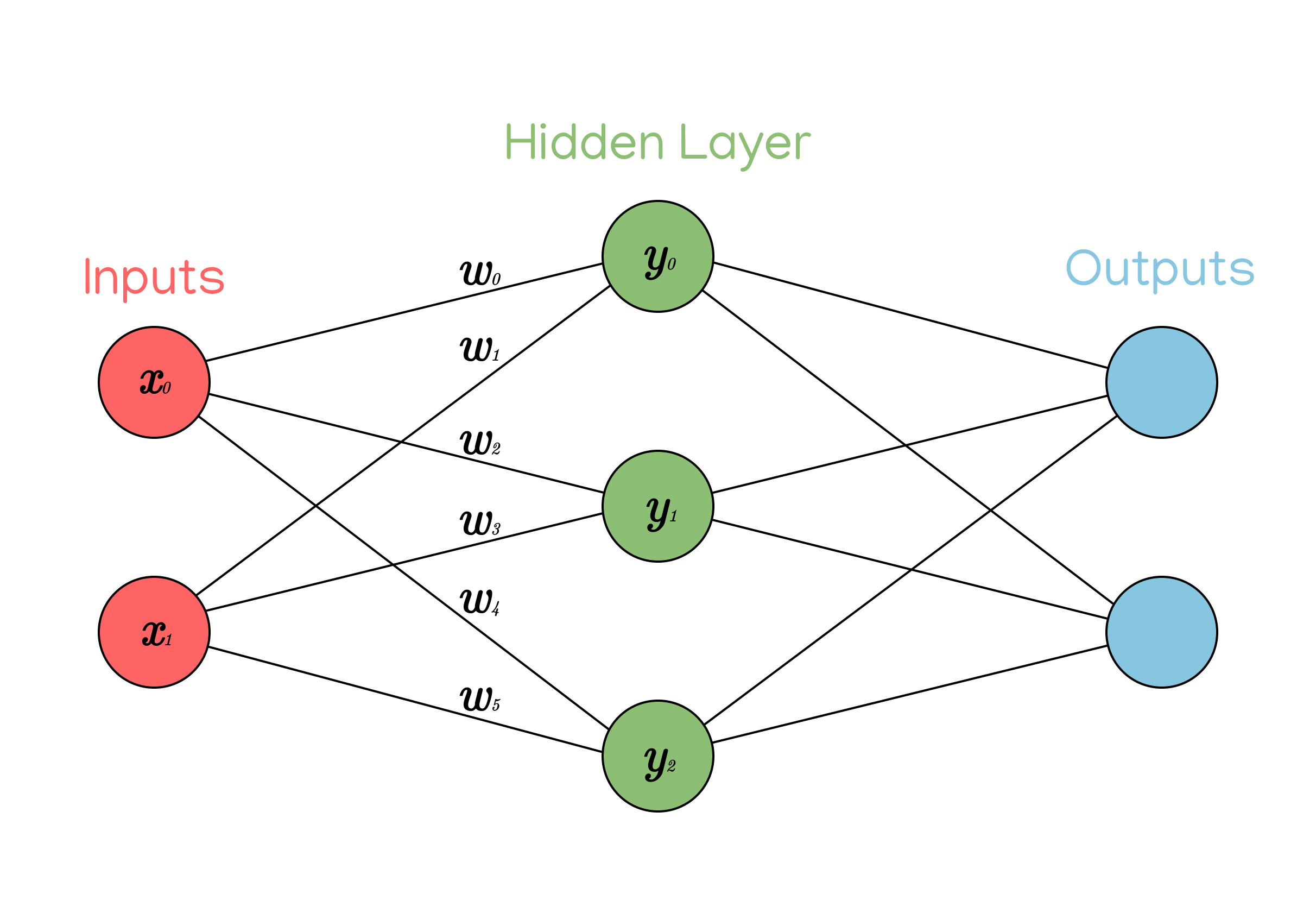
example image

Notice how each neuron has 2 weights. Remember that each weight is just a number, so we can give each neuron its own weight vector to keep track of them.

For example, the weight vector of the neuron \(y_1\) would be

$$\begin{bmatrix}w_2 & w_3\end{bmatrix}$$

Because those are the weights that connect the neuron to its inputs.

Fortunately, since each neuron only has 1 bias, we don’t need to use a vector to represent the bias. We can reference the neuron’s bias using the notation \(b_n\), where \(n\) is the corresponding numbered neuron.

Writing the Layer class

Now that we’ve covered how to represent the neurons’ weights and biases (you’ll see why in a minute), we can start writing the code for the Layer class. We’ll start by declaring a very basic constructor method:

class Layer:
    def __init__(self, num_inputs, num_neurons):
        # ...

You’ll notice that the class takes two arguments: num_inputs, for the number of input neurons, and num_neurons, for the number of neurons in the layer.

We need num_inputs to define the right number of weights per neuron in the layer, and we need num_neurons to know the right number of neurons that we need to define weights for.

The reason we need these parameters is to create a weight matrix. This is essentially a vector of all the neurons’ weights. For instance, since each neuron’s weights are represented by a vector, to represent the weights of all the neurons in the layer, we would need a vector of those vectors, or a matrix.

For example, the weight matrix of the model from above would be:

$$ \begin{bmatrix} w_0 & w_1 \\ w_2 & w_3 \\ w_4 & w_5 \end{bmatrix} $$

You can see how each row in the matrix represents a neuron, and each column represents one of the neuron’s weights. Thus, the number of rows in the matrix is equal to the number of neurons, and the number of columns is equal to the number of weights per neuron, which is equal to the total number of inputs.

Making sense?

So, now we can randomly initialize all the weights for our neurons at once by creating a matrix with dimensions num_neurons * num_inputs. Check out the following code:

class Layer:
    def __init__(self, num_inputs, num_neurons):
        self.weights = np.random.randn(num_neurons, num_inputs)
        # ...
Note: np.random.randn() is a numpy function that returns samples from a standard normal distribution. By passing matrix dimensions as arguments, the function is able to populate an entire matrix with random values. You can view the documentation for np.random.randn() here.

We can do something similar with the biases, though we only need a vector to hold all the biases for the layer because each neuron only has one bias.

class Layer:
    def __init__(self, num_inputs, num_neurons):
        self.weights = np.random.randn(num_neurons, num_inputs)
        self.biases = np.random.randn(num_neurons)

Calculating neuron values (and code!)

By representing weights, inputs, and biases using matrices like above, we can speed up the network significantly and calculate the values of every neuron at once, instead of individually like we were doing in part 2.

To do this, we can find the dot product of the inputs and weights.

$$ X = I * W + B $$

Note: in the future, I’ll write a more in-depth post on what a dot product is, how to compute a dot product, and their application in neural networks, but for now, I think the mathisfun guide does a pretty good job explaining.

We can represent this in code by defining a method to our Layer class that returns the dot product of its inputs and weights (and adds the biases) using the numpy function np.dot().

class Layer:
    def __init__(self, num_inputs, num_neurons):
        self.weights = np.random.randn(num_neurons, num_inputs)
        self.biases = np.random.randn(num_neurons)
    def calc_neuron_outputs(self, inputs):
        # assert len(inputs) == len(biases)
        return np.dot(inputs, self.weights) + self.biases

As you can see, the method Layer.calc_neuron_outputs() takes a number of inputs (one for each neuron in the layer) and returns a matrix with all the output values of the neurons by computing the dot product of the inputs and weights, and then adding the biases.

That’s as far as I’ll go for now, but keep an eye out for future posts where we’ll dig a little deeper into dot products, batches of inputs, and activation functions.

Other Parts in the Neural Networks Series   ⬇️