Alright – the first step in the process of coding a neural network from scratch is representing the different components of the network in code.
Since the individual neurons form the foundation of the network, I figured we’d start with those.
Before we begin…
It’s important to realize that the network we create isn’t just going to be a singular chain of neurons strung together one-by-one. Instead, we are going to have layers of neurons that interact with each other. Each neuron in each layer will act as an input to each neuron in the next layer, and so on.
This design is not only critical for the functionality of our network, but it will also reduce computation time.
For example, here’s a model of the configuration of neurons (in layers) for a very simple network:
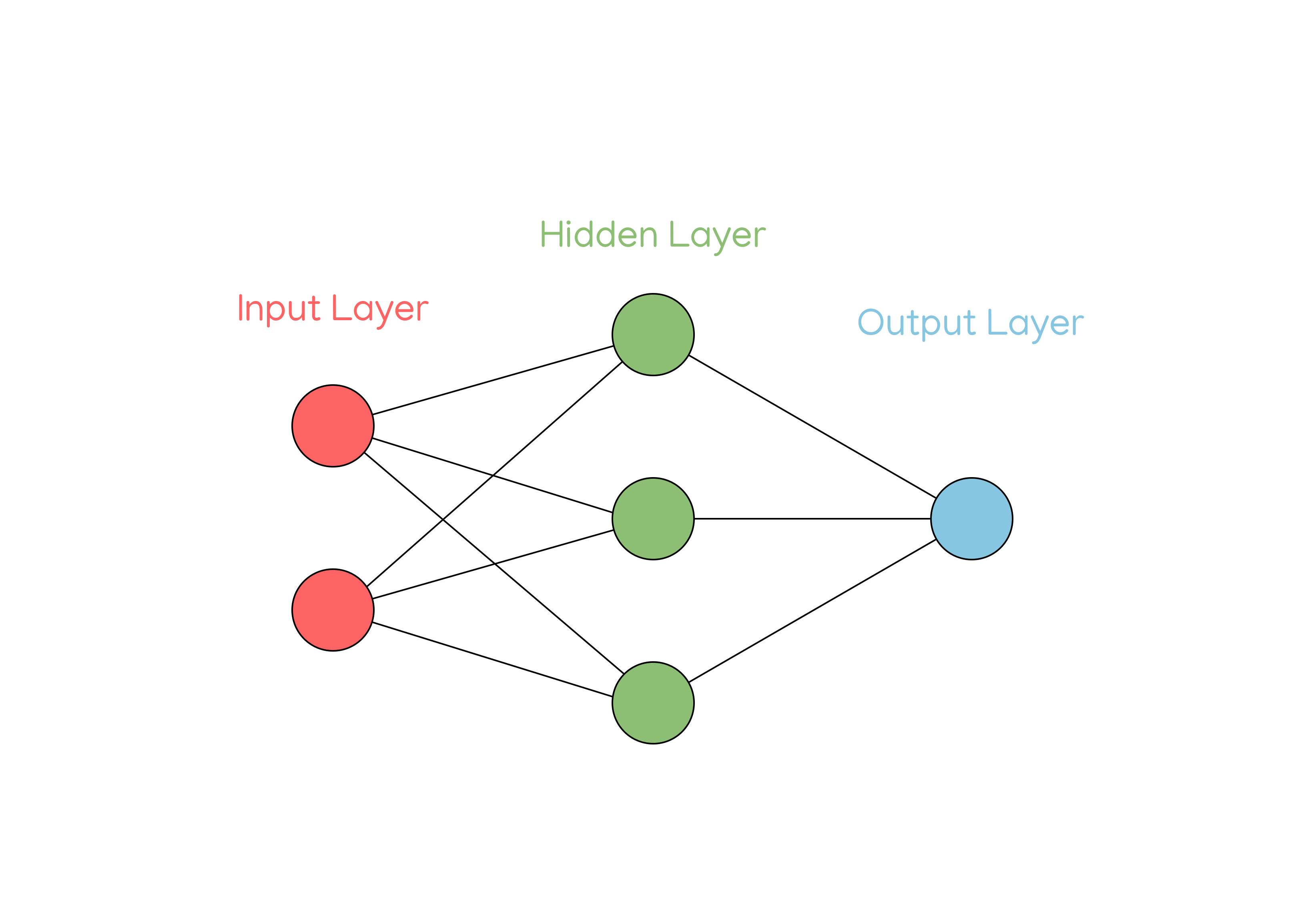
As you can see, there are three layers in this network (also three different types of layers) and six neurons in total.
Each neuron in the network represents a number: the value of that neuron. Each neuron also has other special values called weights and biases that help the network to propagate forward. I’ll get to those later.
I’ll start with the input layer – aptly named, this is the layer of neurons which provide inputs to the network. As you can see, this network takes two inputs.
Realistically, these inputs could be anything: they could be 1s and 0s if the network is built to solve logic gates (like a logical XOR), or they could even be x and y values if the network is intended to predict the output of a mathematical function like sine or cosine.
But what about images? Like I said earlier, each neuron in the network can be boiled down to a numerical value, so to represent images, we generally have a lot of inputs that represent each individual pixel.
For example, if we wanted to input a 64x64 black-and-white image to the network, we would have 4096 inputs for each of the 4096 pixels. Each input would be a value between 0 and 1 to represent the brightness of the pixel it represents.
Next, we have the hidden layer of the network, consisting of 3 neurons. Neural networks can generally have any number of hidden layers consisting of any number of neurons.
Hidden layers are essentially the “logic and reasoning” part of the network - they take the inputs, apply some kind of computation, and then output a value to the output layer.
For example, it’s like baking bread.

The input layer is equivalent to the dough, but the dough has to go in the oven before it becomes a real loaf of bread. Otherwise, it is just a collection of ingredients that have been whisked together.
The hidden layers act similarly. They take the input, mold it and shape it in some way (like the oven for the bread), and then produce an output. The important thing is that the programmer doesn’t really know how the hidden layers are “molding and shaping” the inputs, because the computer learns by itself and creates its own special recipe to get the correct output given an input. It’s like if you put the dough in the oven without knowing what it did and then a complete loaf of bread came out.
Finally, the output layer takes the final product from the hidden layers and then outputs it. The output layer may or may not perform some kind of computation to shape the output, but it ultimately doesn’t change the value of the output. This would be like slicing the bread after it comes out of the oven so it’s ready to eat.
So that’s the basic theory behind how a neural network takes an input and produces an output. There are more intricacies to the layers of the network, and more specific operations to determine the exact values of neurons in the network, but I’ll get into those next time, when we actually start laying out the network’s code.
